AI之梯度下降算法
梯度下降是深度学习的基础,深度学习又是当前AI人工智能领域的底层。
在绝大部分的神经网络模型里有直接或者间接地使用了梯度下降的算法
深度学习的核心:就是把数据喂给一个人工设计的模型,然后让模型自动的“学习”,通过反向传播进而优化模型自身的各种参数,最终使得在某一组参数下该模型能够最佳的匹配该学习任务。那么如果想要这个模型达到我们想要的效果,这个“学习”的过程就是深度学习算法的关键。梯度下降法就是实现该“学习”过程的一种最常见的方式,尤其是在深度学习(神经网络)模型中,BP反向传播方法的核心就是对每层的权重参数不断使用梯度下降来进行优化。虽然不同的梯度下降算法在具体的实现细节上会稍有不同,但是主要的思想是大致一样的。
# 学习要从基础概念抓起
梯度下降的原理
损失函数用来衡量模型的精确度。一般来说,损失函数的值越小,我们训练的模型的精确度就越高。如果要提高模型的精确度,就需要尽可能降低损失函数的值。而降低损失函数的值,我们一般采用梯度下降这个方法。所以,梯度下降的目的,就是最小化损失函数。
也就是求损伤函数最小值的一个过程。
回想我们学习的微分和导数,求一个函数的最小值,最小值的地方应该是导数为0,其他地方的导数要么大于0,要么小于0,想办法找到或者尽量逼近导数为0的值就是我们求解的过程。
一个例子
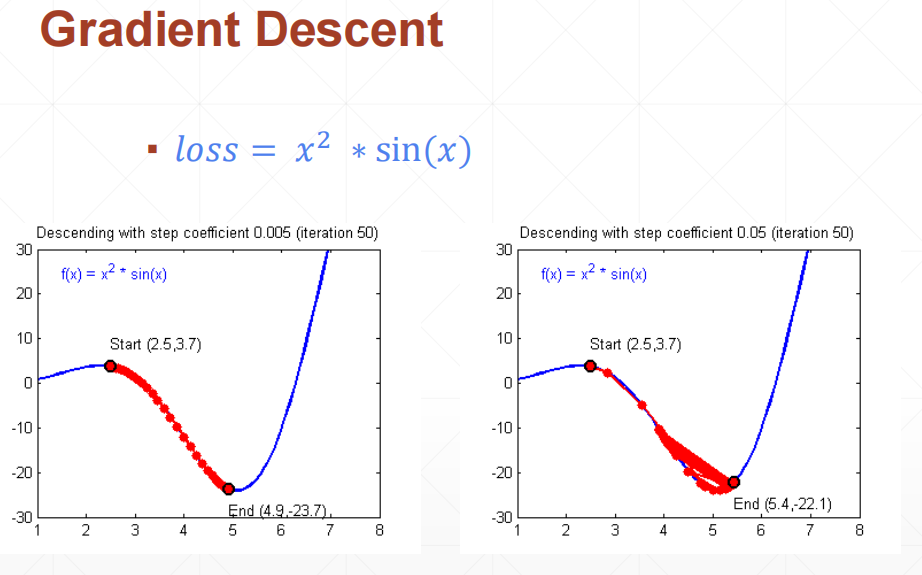
比如这个函数,其导数为 \(2x * sinx+x^2 * cosx\) 显然x=0的时候,此导数为0,但可惜不是最小值,我们要寻找 x>2.5的情况下的最小值
从上图可以看出,在x位于2.5–5之间的时候,其导数为负值,也就是y在不断下降。
如果我们设x=2.5,y=3.7为梯度0,因为导数为负数,假设Δx为导数,那么 x-Δx就会让x朝向极值又移动了一步。为了避免步子迈的太大,就又引入了learning rate:学习率,一般lr会设置的比较小,比如0.001。
这样梯度一就是: \(x = x - Δx * lr\) 这一公式的好处是,如果Δx大于0,这说明步子迈的太大了,超过了最小值点,巧合的是,这时候x会变小,也就是回头,正好还是向着极值的方向。
依次重复下去。。。
这一算法有两个特点:
-
可以求解一定范围内的最小值。当然,前提是这个最小值存在,也就是说这一范围内,该函数应该是凸函数
-
算法具有自动趋向最小值的特征。就像往一个碗里扔一个玻璃球一样,玻璃球总是会自动停在最底部
一个实际应用
看这样一个例子
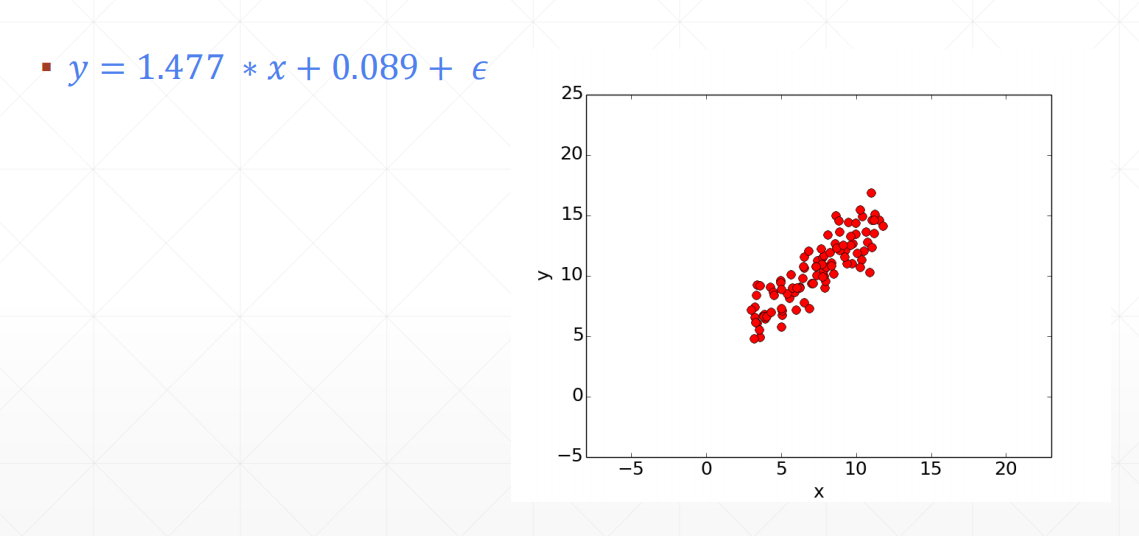
▪ 𝑦 = 𝑤 ∗ 𝑥 + 𝑏
这是一个线性回归的例子,在这个例子里,我们有一组x和y的样本,要拟合出w和b的值。 \(𝑙𝑜𝑠𝑠 = \sum_{i} (𝑤 ∗ 𝑥_𝑖 + 𝑏 − 𝑦_𝑖)^2\) 现在就是要用梯度下降算法求这个损失函数的最小值。
loss对w的导数: \(2(𝑤 ∗ 𝑥_𝑖 + 𝑏 − 𝑦_𝑖) * 𝑥_𝑖\) loss对b的导数: \(2(𝑤 ∗ 𝑥_𝑖 + 𝑏 − 𝑦_𝑖)\)
import numpy as np
# y = wx + b
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
totalError += (y - (w * x + b)) ** 2
return totalError / float(len(points))
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
new_b = b_current - (learningRate * b_gradient)
new_m = w_current - (learningRate * w_gradient)
return [new_b, new_m]
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
b = starting_b
m = starting_m
for i in range(num_iterations):
b, m = step_gradient(b, m, np.array(points), learning_rate)
return [b, m]
def run():
points = np.genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_m = 0 # initial slope guess
num_iterations = 1000
print("Starting gradient descent at b = {0}, m = {1}, error = {2}"
.format(initial_b, initial_m,
compute_error_for_line_given_points(initial_b, initial_m, points))
)
print("Running...")
[b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)
print("After {0} iterations b = {1}, m = {2}, error = {3}".
format(num_iterations, b, m,
compute_error_for_line_given_points(b, m, points))
)
if __name__ == '__main__':
run()
这里的重点就是方法step_gradient(),尤其是里面对新梯度的计算: \(w_{new} = w - Δw * lr = w - 2(𝑤 ∗ 𝑥_𝑖 + 𝑏 − 𝑦_𝑖) * 𝑥_𝑖*lr\)
\[b_{new} = b - Δb * lr = b - 2(𝑤 ∗ 𝑥_𝑖 + 𝑏 − 𝑦_𝑖) * lr\]最终,结果可以很好的拟合:
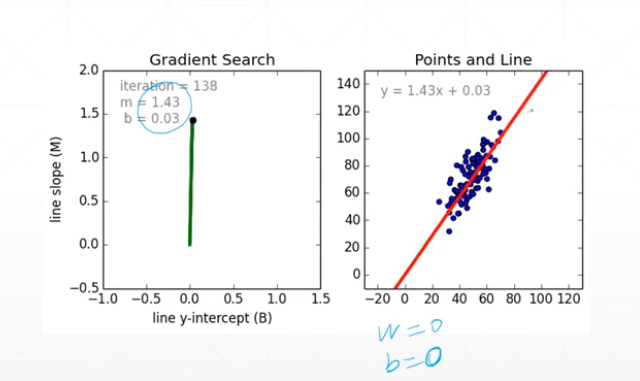
总结
- 梯度下降是人工智能AI的基础,是深度学习的基础
- 理解这几个概念至关重要,包括learning rate,损失函数等
- 这里的例子只是一次的线性函数,如果是二次或者更高,理解会更困难
- 激活函数和逻辑回归还没有太理解,有待以后加强